End of document------
--------GO Up to HOME Page____
--------See the previous Version html Revised July 2021
ABSTRACT:
A Construction Proof of Prime Number Sums forming numerical and graphic patterns in both 2D and 3D when unit stepped by the golden ratio logarithm! This sequential three dimensional sum of Primes forms all possible Volumes precisely.
The shape of Volume that emerges is a exact Dodecahedron .

Non-technical Introduction
Prime Numbers parallel the history of Mathematics and Number theory.
Their what and why have intrigued most of the pioneers of mathematics and led to many other discoveries and mathematical techniques.
Their seemingly random nature coupled with their infinite range have fascinated and driven both early and modern mathematics.
The modern approach is the Riemann Hypothesis (RH) which endeavors to prove via the Complex Plane based Zeta function that all Primes have a common attribute; all lie on the critical line defined by their real component being exactly equal to one over two (1/2),
The objective of the RH is to account for the exact number of Primes in any given range, among others.
This has been shown to be true for the first several billion Primes by calculation of their Zeta function.
However, no method has emerged that proves it over an infinite range. The significance of the RH allows the number of Primes in any range to be precise. Many modern mathematical ideas arise in assuming the RH is true.
The Riemann Zeta function is based on the formal function "Zeta( i^2) = -1/12" .
Remember this Zeta "12" constant when conclusions are presented below.
This is discovery is about the Fundamentals of Geometry and Mathematics; one that answers the "What and Why" of Primes.
Accumulating the primes reveals values that explain the how and why of PN distribution; when Golden Ratio logs are used.
Assuming that "Twelve" and Primes have only that one sterile Zeta interpretation;
completely misses how the dodecahedron's volume 12ths fit so beautifully to the PN sums.
Assumptions & Hypothesis
In re-examining the concepts of NUMBER, quantity is its understood fundamental.
Therefore, assuming Prime Numbers are three-dimensional in nature seems conservative.
Since Volume is the essence of summation of smaller volumes, it is all very three dimensional!
Prime Number Sums then take on special significance with the assumption that Prime Numbers are three dimensional in nature.
A close analogy is that Prime Numbers are discrete pieces of Volume and their Sums represent the total accumulated Volume.
If the assumption is correct, then Prime Number sums should reveal their three-dimensional nature in some strong numerical and geometrical fashion.
Table of Contents
Results for the first 1300 Million Primes Sums
After examining the first 10 million Prime Number (PN) sums using most log bases,
no patterns but one emerge that support a three-dimensional basis.
When the golden ratio [ P = 1.618... ] is used as the log base [Lp], a clear and repeating pattern in both 2D and 3D emerges; as graphed in the following images.
The appended Table reveals a regular pattern.
It was found by summing the first 1300 Million Primes and noting their sums based on Lp unit steps.
This P or Lp +1 snapshot perspective reveals two more resonances at P^3 and P^4 steps
that slowly change predictably.
The six column Table lists the step count, the Prime at that step (PN),
the sum of all Primes to that step and its Golden Ratio log Lp,
the Top plane and the ratio of the PN times the step, divided by the sum.
The TOP plane value is the Lp of the Dodecahedron edge.
The DATA
For example, the Table's last five Lp+3 values are:
Step:73629340 PN:1476842981 Sum:5.293618e+16 its Lp:80.0227 & TOP Plane:A27.004978 *-12
Step:148739879 PN:3093685613 Sum:2.242413e+17 its Lp:83.0227 & TOP Plane:A28.004978 *-9
Step:300679579 PN:6476687027 Sum:9.499013e+17 its Lp:86.0227 & TOP Plane:A29.004978 *-6
Step:608217668 PN:13551217079 Sum:4.023847e+18 its Lp:89.0227 & TOP Plane:A30.004978 *-3
Step:1231043204 PN:28338246133 Sum:1.704529e+19 its Lp:92.0227 & TOP Plane:A31.004978 *
At the -end- Step of 1299,145937, the Sum is 19,031054,505862,185106 with Lp of 92.251689
The ratio of (Step* PN) / SUM slowly falls towards TWO as the SUM grows.
For example, the last table entry at A31.004978 has a ratio of ( (1231043204 * 28338246133 ) / 1.704529e+19) = 2.046642~.
The 2D mapping [right side fig]
The last 4 step sums are mapped between 5 top planes
at scales A27, A28, A29, A30 and A31 ; A27 is P^-4 smaller than A29.
Graphing A31 down to A27 had 3 interior zones in a d2 array.
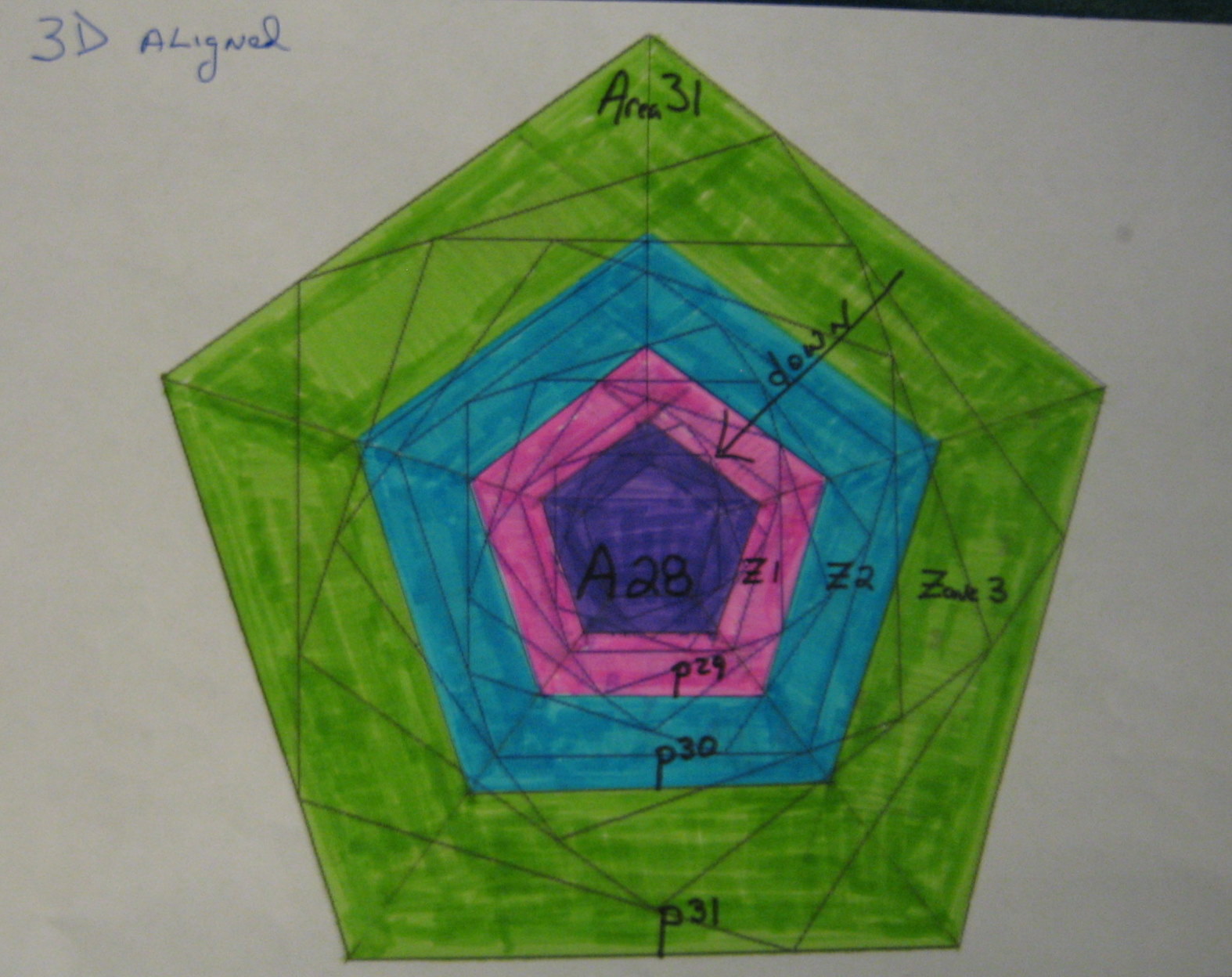
The 3D mapping [left side fig]
The last 3 step sums are mapped between 4 top planes
at scales A28, A29, A30 and A31 ; A31 is P^2 larger than A30.
Graphing A31 down to A28 had 3 interior zones in a d3 array.
Table of Contents
Some Spatial Perspectives
This paper uses the following dimensions to empathize very small scales:
P^0 = 1 fm & P^12 = 321.996 fm, this makes the data's P^31 equal to 3.010349e6 fm
and its area was A31 at 15.5913122 e12 fm^2 [ fm = 10^-13 cm ].
The reason the Lp's can not increase by exactly one, is that Lp(primesum) steps from less than, to over one,
based on the last prime integer added.
Table of Contents
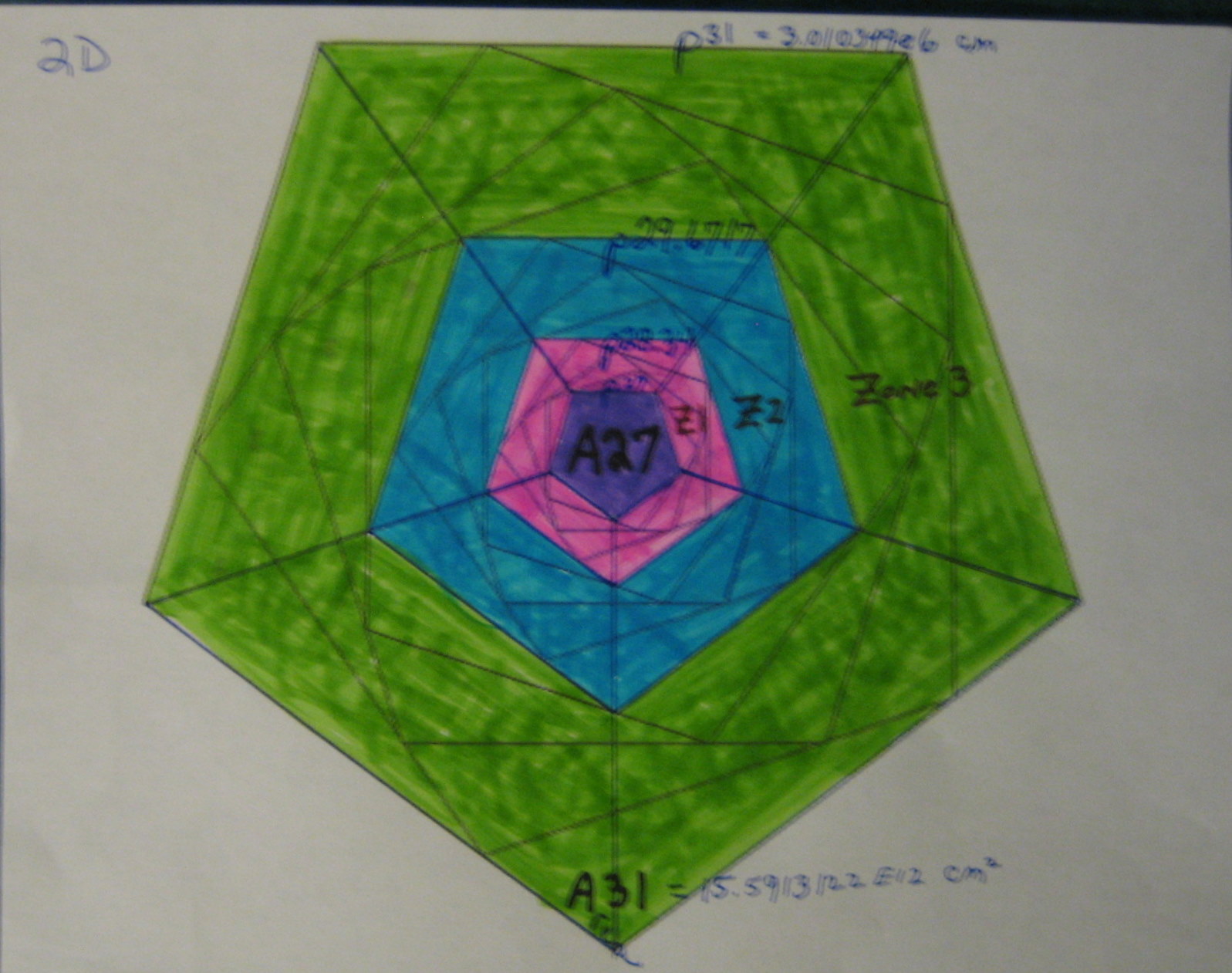
The 2D figure on the right shows a linear four-step pattern between the last five Top Planes; this pattern is purely two-dimensional in Nature.
The 3D figure on the left illustrates the three zones between the four Top Planes.
These zones or cross sections are called "VECTIONs".
The Green Vection is P^3 larger than the Blue Vection
which is P^3 larger than the Red Vection; the Green Vection is (P^6) ~18 times larger than the Red Vection.
Table of Contents
Conclusions
All of the criteria of PNs being three dimensional are met proving the following:
- Th PN sequential sum forms a three dimensional Zeta based shape
- Sum times fifth power of Golden Ratio [ P^5 ] forms a geometrically precise Dodecahedron volume
- The edge of the Dodecahedron is the Zeta shape Top Plane value
- All volumes are formed due to the unlimited nature of Primes
The mathematical proof examples and details
It is TRUELY amazing that Prime Number Sums are simultaneously one, two and three-dimensional in nature!
But only if you use the Golden ratio as your Log base does the pattern emerge.
Both the three_N and four_N step Lp Patterns of the Prime Sums are clearly real and definitive!
The Zeta pattern of the PN sum will go on to Infinity due to infinite nature of PNs!
As for larger Prime sums being consistent with this theory,
this site's 10^20 data is very much in harmony with this paper.
For example, there are 2,220819,602560,918840 primes that sum to
109,778913,483063,648128,485839,045703,833541. its Lp of 182.02282~ and Top Plane 60.98494~.
It has a 2.023~ value for its ((Step * PN )/ SUM) .
This paper makes the RH quest moot in so far as Prime Number distribution, since the data table below clearly accounts for
the EXACT distribution of the Prime Numbers via the golden log of their running sum!
Therefore Prime Numbers and their distribution as three-dimensional sums follows {Q.E.D.} from these Prime Sums and Graphic Proofs!
Putting the patterns together reveals the generic regular three-dimensional shape of the data as seen in this Tone31.0 image.

The Tone: a Five sided Zeta cone!
Twelve of these Tones combined, form the 3D shape known as a Dodecahedron [shown below].
It has six axes and is much more precise; both in orientation and volume; no right-angles needed.
Recalling that the Zeta function is based on 12ths, an extremely strong linkage becomes apparent between them.
The Correlation between the Zeta function and the graphic pattern proofs of these Prime Number Sums,
might be accounted for, by assuming some relationship with Zeta's "Euler Product".
A. Wiles proof relies on elliptic curves which are also three-dimensional in nature just as the Primes seem to be.
Here is a paper I used that proves that the Primes contain arbitrarily long arithmetic progressions.
Table of Contents
Conjecture(s) & Discussion(s)
The assumption that Prime Number magnitude can be modeled as a dodecahedron as well as X, Y, & Z based coordinates is literally proven,
by using six(6) sided cubic Dice UNITs to fill any Prime sized volume.
eg. PN 17 as 17 cubic units, PN 997 as 997 cubic units, etc .
A three-dimensional perspective then emerges that illustrates how Volume can be fitted or filled exactly.
This discovery's regularity could account for the RH Zeta's offset regularities:
Zeta's RH interpretation might be D2 projections of the D3 patterns that emerge, as shown in the tables below.
And Yes, of course, even more, new questions arise
concerning these new and different aspects of Number Theories and VOLUME as Quanta.
Yet, it is possible to assume most unspecified Numbers are geometrically three-dimensional,
with special rules for small values and areas, based on this data.
Table of Contents
Encryption Usages
Another interesting item is that there seem to be two types of Prime Numbers (PNs);
a PN can be either an ordinary one or the sum of PNs. For example,
All the 41596 PN's up to and including 500729 sum to 9.943257281e9 which is also a PN, but much larger.
And all the 63420 PN's up to and including 792731 sum to 2.4042793771e+10 which is also a very much larger PN.
There are endless PN sum table patterns possible, most usable as PRNG's and Encoders;
simply by biasing the generator and/or slewing its axis.
A possible Public Key system could be built using the 3 unique values of Step, PN, and its SUM;
when the SUM is also a Prime; making for a large unique Triple point.
This could be the basis for a "Trap-door" function starting point, to be used as Markers for a unique set of keys.
The user would select several of these Triple Markers from a list which is locally generated.
Here are two examples:
2016th Triple is PN:500729 its SUM:9.943257281e9 at Step:41596
2943th Triple is PN:792731 its SUM:2.4042793771e+10 at Step:63420
--------------------------------
A custom algorithm would be used to combine a user-ID-Key with the message/topic/security selected Triples,
to generate a unique local master Table file whose sum is its message Parity
The generated Table is then used to code or decode designated content using the Table's unique sequence of Prime Numbers.
Table of Contents
Golden Ratio Logs
The Golden ratio was chosen because it has all three-ratios simultaneously:
length increases by P^1=1.618... , area by P^2=2.618... and volume by P^3=4.23606... ;
also note that P^2 = P^1 + 1 and that it is close to 'e' ,
and P^3 = 4 + P^-3 or 4 = P^3 - P^-3.
Lp is the log to base ( sqrt(5) + 1 ) / 2 ) = 1.618...,
Lp(X) = log( X ) / log(1.618....) .
Here are some common Lp examples:
Lp(123) = 10.000137.. ; and the inverse Px(10) = 122.991....
Lp(10) = 4.784972~ Lp(pi) = 2.37885~, Lp(e) = 2.078087~, Lp(2) = 1.44042~.
Px(5) = 11.090169943749~ , Lp(c) = 50.1313~ with P^0 = one centi-metre [cm]
An arbitrary scale of one centimeter reference for the powers of Px, was selected for our human scale;
eg. P^11 is 199.005 cm or 6.53 feet.
Lucas numbers represent the integer steps of Px(n) series;
29, 47, 76, 123, 199 are the 7th, to 11th Lucas numbers.
The 3D rotated and 3D aligned pair are shown on the right.

Afterword
I credit my Computer System Skills and Tools, along with my Geometrical insights, in making this discovery possible.
And to Pythagoras, who boasted that the Dodecahedron secrets described the Universe's essences.
The data shows that Prime Numbers filled them exactly when framed as 12ths of a DodecaHedron!
See my site for the latest material. WEB Site"
RD OMeara Oak Park IL October 2010 to 2021
Table of Contents
---------------TABLE of Prime Number Sums------See the Proof section for new revised table------------
1ST 1300 Million Prime Sums arranged by Lp, the log of 'P' the golden ratio!
Jan 2021 Author: RD_OMeara @ 60302
Step:1 PN:2 Sum:2.000000000000000e+00 its Lp:1.440420 & TOP Plane:A0.000000 (Step*PN)/Sum= 0.000000
Step:167 PN:991 Sum:7.513000000000000e+04 its Lp:23.330630 & TOP Plane:A8.293903 (Step*PN)/Sum= 2.202808
Step:342 PN:2297 Sum:3.609790000000000e+05 its Lp:26.592395 & TOP Plane:A9.381407 (Step*PN)/Sum= 2.176232
Step:467 PN:3319 Sum:7.108360000000000e+05 its Lp:28.000553 & TOP Plane:A9.850791 (Step*PN)/Sum= 2.180493
Step:584 PN:4259 Sum:1.153779000000000e+06 its Lp:29.007087 & TOP Plane:A10.139662 (Step*PN)/Sum= 2.155747
Step:730 PN:5521 Sum:1.869711000000000e+06 its Lp:30.010265 & TOP Plane:A10.372104 (Step*PN)/Sum= 2.155590
Step:913 PN:7127 Sum:3.027278000000000e+06 its Lp:31.011654 & TOP Plane:A10.669106 (Step*PN)/Sum= 2.149440
Step:1142 PN:9209 Sum:4.901431000000000e+06 its Lp:32.013007 & TOP Plane:A11.002360 (Step*PN)/Sum= 2.145634
---- Note the three Lp step sequences have a plus one Top Plane sequence
Step:1430 PN:11933 Sum:7.938735000000000e+06 its Lp:33.015117 & TOP Plane:A11.336286 (Step*PN)/Sum= 2.149485
Step:1791 PN:15329 Sum:1.285766600000000e+07 its Lp:34.017142 & TOP Plane:A11.670360 (Step*PN)/Sum= 2.135243
Step:2244 PN:19841 Sum:2.081248500000000e+07 its Lp:35.017975 & TOP Plane:A12.003918 (Step*PN)/Sum= 2.139255
Step:2813 PN:25541 Sum:3.369458800000000e+07 its Lp:36.019164 & TOP Plane:A12.337553 (Step*PN)/Sum= 2.132296
Step:3527 PN:32911 Sum:5.454920800000000e+07 its Lp:37.020316 & TOP Plane:A12.671180 (Step*PN)/Sum= 2.127934
Step:4424 PN:42323 Sum:8.827670500000000e+07 its Lp:38.020651 & TOP Plane:A13.004574 (Step*PN)/Sum= 2.121023
Step:5551 PN:54547 Sum:1.428682720000000e+08 its Lp:39.021139 & TOP Plane:A13.337998 (Step*PN)/Sum= 2.119368
Step:6968 PN:70309 Sum:2.312054110000000e+08 its Lp:40.021496 & TOP Plane:A13.671369 (Step*PN)/Sum= 2.118952
Step:8749 PN:90371 Sum:3.741730820000000e+08 its Lp:41.021912 & TOP Plane:A14.004849 (Step*PN)/Sum= 2.113075 &
Step:10989 PN:116329 Sum:6.054897820000000e+08 its Lp:42.022135 & TOP Plane:A14.338229 (Step*PN)/Sum= 2.111248
Step:13806 PN:149497 Sum:9.797281690000001e+08 its Lp:43.022188 & TOP Plane:A14.671549 (Step*PN)/Sum= 2.106661
Step:17350 PN:192259 Sum:1.585260063000000e+09 its Lp:44.022223 & TOP Plane:A15.004855 (Step*PN)/Sum= 2.104193
Step:21811 PN:247229 Sum:2.565107180000000e+09 its Lp:45.022306 & TOP Plane:A15.338201 (Step*PN)/Sum= 2.102178
Step:27425 PN:317789 Sum:4.150598044000000e+09 its Lp:46.022390 & TOP Plane:A15.671566 (Step*PN)/Sum= 2.099785
Step:34496 PN:408533 Sum:6.716063735000000e+09 its Lp:47.022469 & TOP Plane:A16.004930 (Step*PN)/Sum= 2.098365
Step:43398 PN:524389 Sum:1.086707883100000e+10 its Lp:48.022518 & TOP Plane:A16.338276 (Step*PN)/Sum= 2.094163
Step:54612 PN:673979 Sum:1.758381641900000e+10 its Lp:49.022579 & TOP Plane:A16.671628 (Step*PN)/Sum= 2.093251
Step:68738 PN:865259 Sum:2.845129135500000e+10 its Lp:50.022585 & TOP Plane:A17.004955 (Step*PN)/Sum= 2.090456
Step:86537 PN:1111091 Sum:4.603566510400000e+10 its Lp:51.022608 & TOP Plane:A17.338294 (Step*PN)/Sum= 2.088609
Step:108970 PN:1426693 Sum:7.448777308100000e+10 its Lp:52.022622 & TOP Plane:A17.671627 (Step*PN)/Sum= 2.087144
Step:137244 PN:1831033 Sum:1.205246911950000e+11 its Lp:53.022638 & TOP Plane:A18.004967 (Step*PN)/Sum= 2.085036
Step:172893 PN:2350237 Sum:1.950136972540000e+11 its Lp:54.022645 & TOP Plane:A18.338301 (Step*PN)/Sum= 2.083646
Step:217836 PN:3015113 Sum:3.155387957710000e+11 its Lp:55.022645 & TOP Plane:A18.671632 (Step*PN)/Sum= 2.081519
Step:274517 PN:3868279 Sum:5.105561022180000e+11 its Lp:56.022660 & TOP Plane:A19.004971 (Step*PN)/Sum= 2.079905
Step:346004 PN:4961783 Sum:8.260999344950000e+11 its Lp:57.022667 & TOP Plane:A19.338306 (Step*PN)/Sum= 2.078195
Step:436185 PN:6364637 Sum:1.336660431700000e+12 its Lp:58.022671 & TOP Plane:A19.671641 (Step*PN)/Sum= 2.076937
Step:549959 PN:8162513 Sum:2.162767782660000e+12 its Lp:59.022677 & TOP Plane:A20.004976 (Step*PN)/Sum= 2.075603
Step:693515 PN:10466471 Sum:3.499432331226000e+12 its Lp:60.022677 & TOP Plane:A20.338308 (Step*PN)/Sum= 2.074238
Step:874686 PN:13418147 Sum:5.662201245143000e+12 its Lp:61.022677 & TOP Plane:A20.671641 (Step*PN)/Sum= 2.072810
Step:1103334 PN:17201237 Sum:9.161645774013000e+12 its Lp:62.022680 & TOP Plane:A21.004975 (Step*PN)/Sum= 2.071539
Step:1391966 PN:22044949 Sum:1.482387241233500e+13 its Lp:63.022682 & TOP Plane:A21.338310 (Step*PN)/Sum= 2.070027
Step:1756332 PN:28255313 Sum:2.398553891705500e+13 its Lp:64.022683 & TOP Plane:A21.671643 (Step*PN)/Sum= 2.068985
Step:2216382 PN:36211757 Sum:3.880941935961100e+13 its Lp:65.022683 & TOP Plane:A22.004976 (Step*PN)/Sum= 2.068031
Step:2797290 PN:46393433 Sum:6.279500190146700e+13 its Lp:66.022685 & TOP Plane:A22.338310 (Step*PN)/Sum= 2.066659
Step:3530896 PN:59441509 Sum:1.016044827550970e+14 its Lp:67.022685 & TOP Plane:A22.671644 (Step*PN)/Sum= 2.065674
Step:4457435 PN:76142323 Sum:1.643995443928520e+14 its Lp:68.022686 & TOP Plane:A23.004977 (Step*PN)/Sum= 2.064479
Step:5627751 PN:97536821 Sum:2.660041170975360e+14 its Lp:69.022686 & TOP Plane:A23.338311 (Step*PN)/Sum= 2.063551
Step:7106165 PN:124926157 Sum:4.304037267433580e+14 its Lp:70.022687 & TOP Plane:A23.671644 (Step*PN)/Sum= 2.062589
Step:8973934 PN:159989891 Sum:6.964079995717210e+14 its Lp:71.022687 & TOP Plane:A24.004977 (Step*PN)/Sum= 2.061634
Step:11333855 PN:204873829 Sum:1.126811918555114e+15 its Lp:72.022687 & TOP Plane:A24.338311 (Step*PN)/Sum= 2.060690
Step:14315833 PN:262319557 Sum:1.823220018613568e+15 its Lp:73.022687 & TOP Plane:A24.671644 (Step*PN)/Sum= 2.059720
Step:18084223 PN:335866043 Sum:2.950031982530104e+15 its Lp:74.022687 & TOP Plane:A25.004977 (Step*PN)/Sum= 2.058919
Step:22846796 PN:429975173 Sum:4.773252037356833e+15 its Lp:75.022687 & TOP Plane:A25.338311 (Step*PN)/Sum= 2.058042
Step:28866367 PN:550420693 Sum:7.723284548833266e+15 its Lp:76.022687 & TOP Plane:A25.671644 (Step*PN)/Sum= 2.057239
Step:36475354 PN:704526727 Sum:1.249653714936846e+16 its Lp:77.022687 & TOP Plane:A26.004978 (Step*PN)/Sum= 2.056399
Step:46094125 PN:901746253 Sum:2.021982246882949e+16 its Lp:78.022687 & TOP Plane:A26.338311 (Step*PN)/Sum= 2.055666
Step:58254572 PN:1154047031 Sum:3.271636101805701e+16 its Lp:79.022688 & TOP Plane:A26.671644 (Step*PN)/Sum= 2.054890
Step:73629340 PN:1476842981 Sum:5.293618436879220e+16 its Lp:80.022688 & TOP Plane:A27.004978 (Step*PN)/Sum= 2.054152 *-12
Step:93069728 PN:1889788871 Sum:8.565254595481313e+16 its Lp:81.022688 & TOP Plane:A27.338311 (Step*PN)/Sum= 2.053437
Step:117652380 PN:2418027719 Sum:1.385887306143076e+17 its Lp:82.022688 & TOP Plane:A27.671644 (Step*PN)/Sum= 2.052741
Step:148739879 PN:3093685613 Sum:2.242412777300252e+17 its Lp:83.022688 & TOP Plane:A28.004978 (Step*PN)/Sum= 2.052050 *-9
Step:188056076 PN:3957867593 Sum:3.628300105865439e+17 its Lp:84.022688 & TOP Plane:A28.338311 (Step*PN)/Sum= 2.051377
Step:237782434 PN:5063171261 Sum:5.870712922157453e+17 its Lp:85.022688 & TOP Plane:A28.671644 (Step*PN)/Sum= 2.050744
Step:300679579 PN:6476687027 Sum:9.499013098873580e+17 its Lp:86.022688 & TOP Plane:A29.004978 (Step*PN)/Sum= 2.050116 *-6
Step:380241003 PN:8284239937 Sum:1.536972612829301e+18 its Lp:87.022688 & TOP Plane:A29.338311 (Step*PN)/Sum= 2.049489
Step:480888447 PN:10595705777 Sum:2.486873937064963e+18 its Lp:88.022688 & TOP Plane:A29.671644 (Step*PN)/Sum= 2.048899
Step:608217668 PN:13551217079 Sum:4.023846558113720e+18 its Lp:89.022688 & TOP Plane:A30.004978 (Step*PN)/Sum= 2.048311 *-3
Step:769312187 PN:17330081771 Sum:6.510720512633547e+18 its Lp:90.022688 & TOP Plane:A30.338311 (Step*PN)/Sum= 2.047737
Step:973137428 PN:22161454589 Sum:1.053456708922355e+19 its Lp:91.022688 & TOP Plane:A30.671644 (Step*PN)/Sum= 2.047179
Step:1231043204 PN:28338246133 Sum:1.704528763297476e+19 its Lp:92.022688 & TOP Plane:A31.004978 (Step*PN)/Sum= 2.046642 *
-end- Step:1299145937 Prime:29979245999 Sum:1.903105e+19 Lp:92.251689 idx:68 Base=27.000000 bias=0.000000
PNSUM 19031054505862185106
---- Run check values -------
mark 1e6 at step:78497 PN : 999979 Sum: 3.754940E+10 Lp: 50.599179
mark 1e9 at step:50847533 PN : 999999929 Sum: 2.473951E+16 Lp: 78.441917
mark 1e10 at step:455052510 PN : 9999999943 Sum: 2.220822E+18 Lp: 87.787554
at step 1000000000, PN is 22801763489 sum Lp 91.138528
Table of Contents
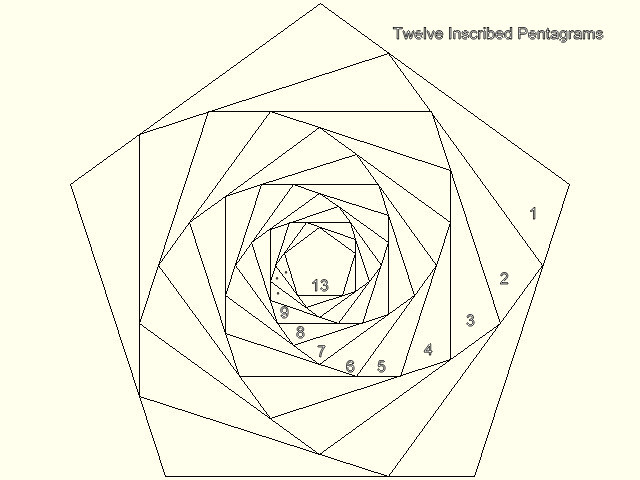
This image on the right illustrates 12 inscribed pentagons which allow both the 3 and 4 step Lp planes
to be visualized as seen in the table's data.
It was used to highlight the patterns found in the Table of Prime number Sums
Table of Contents
Appendix: Volume and Scale
Let a cubic centimeter [or cc = cm^3] be the standard volume unit. On our human scale, this small sugar cube sized item seems small and ordinary.
What does Mercury's orbital volume of 8e23 KM^3 and the Nuclear scale's 10^-39 cm^3 volume have in common
with this standard cm^3 ?
Both are equally distant from a standard cubic centimeter;.
Imagine this cubic cm as the mid zone volume between Nuclear and Planetary Orbit scale volumes.
This means the volume of Mercury's orbit is as distant as the volume of a nucleus when using a
cubic cm reference volume.
Compare it at whatever precision imaginable.
Pause to consider how planetary orbital volumes makes any human scale volume seem insignificant;
whether it's a cubic cm or a cubic mile.
Can any basis of linearity be possible or even imaginable at these vast ranges?
Surely VOLUME at the Nuclear scale and solar orbital scale would be things onto themselves.
Normal spatial concepts of our macro scale would seem not apply over such a vast scale distance.
Users of Nano technology are familiar with non-linear scale effects that redefine our common macro sense of volume.
For example, static electricity effects dominate for surfaces and shapes at a mere billionth of our scale.
See the Links below for my formal thoughts on Space and Mass.
Table of Contents
LINKS 
author: RD O'Meara Oak Park, IL.
This WEB page address: "http://mister-computer.net/primesums/Primes3D.htm"
Email of Author: 'RDo.meara@mister-computer.net'
Monopole Aether Theory: A Neo-Classical model of the Aether based on monopole pairs .
5SPACE : "Stable Particle Masses mapped by (N/2)^5, N=1 to 22"
JID's SLOPE: The Universal Slope of Volume,
both Mathematically and Physically being the Rydberg constant of 1.0973~!
Short proof of Fermat's FLT: A proof based on power sequences infinite transcendental Logs.
My Real interests are in computer science.
I have spent my career as a cybernetic engineer/designer
who is concerned about the future of our digital data.
Our entire cyber infrastructure lacks "Data Sanity";
especially in the areas of forgery and security, for data and their time stamps.
In that vein, I am seeking venture capital for my NEW multi-Computer
Distributed Kernel SECURITY Architecture or 'DSA' ; based on
Posopip: a 3CPU template that inherently guarantees Trust & Fidelity.
Table of Contents
Oct2010
