End of document------
--------GO Up to HOME Page
-------->

See the final Version: Primes3D.htm -
A Construction Proof of How ALL Primes are three-dimensional!
ABSTRACT: Prime Number Sums form a pattern when stepped by the golden ratio logarithm!

Results for the first 300 Million Primes Sums
It is well known that Prime Number attributes are logarithmic and that
they form an upward spiral in some fashion.
This image illustrates 12 inscribed pentagons which allows both the 3 and 4 step Lp planes to be visualized ; as seen in the table's data.
It will be used to highlight the patterns found in the Table of Prime number Sums
The appended Table reveals a regular pattern.
It was found by summing the first 300 Million Primes
and noting their sums based on Lp unit increments.
This P^1 or Lp +1 snapshot perspective reveals
two more resonances at P^3 and P^4 steps
that seem to slowly change predictably.
The six column Table lists the step count,
the PN/step ascending ratio and the Prime at that step: PN,
the sum of all Primes to that step and its Golden Ratio log Lp,
and the TOP plane at that step derived from the P^3 growth.
Also noted was the minor PN/Step ratio takes four Lp steps
to increase by almost one.
For example, the Table's last five Lp+3 values 2 are:
Step:18084223 PN/Step:18.572324 PN:335866043 Sum:2.950032E15 its Lp:74.022687 & Plane:A25.004977
Step:36475354 PN/Step:19.315144 PN:704526727 Sum:1.249653E16 its Lp:77.022687 & TOP plane:A26.004978
Step:73629340 PN/Step:20.057806 PN:1476842981 Sum:5.293618E16 its Lp:80.022688 & TOP plane:A27.004978
Step:148739879 PN/Step:20.799302 PN:3093685613 Sum:2.242412E17 its Lp:83.022688 & TOP plane:A28.004978
Step:300679579 PN/Step:21.540163 PN:6476687027 Sum:9.499013E17 its Lp:86.022688 & TOP plane:A29.004978
Where the Sum is 9.499013E17, its Lp is 86.0227~
And the PN/Step is 6476687027 / 300679579 = 21.540163 .
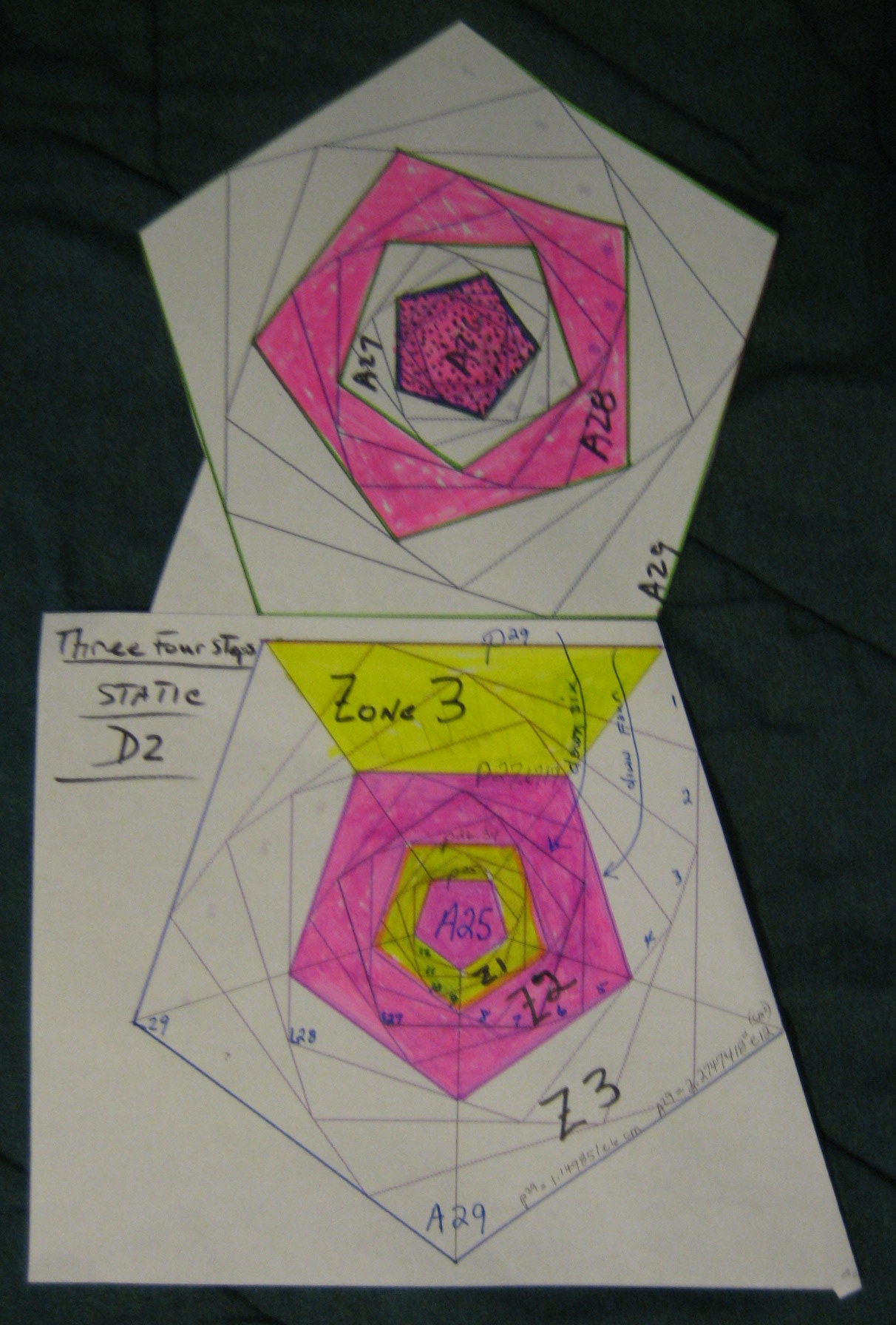
The last 4 step sums are mapped between 5 top planes
at scales A25, A26, A27, A28 and A29 ; A25 is P^-4 smaller than A27.
Graphing A25 up to A29 had 3 interior zones ; all d2, all just areas.
The last 3 step sums are mapped between 4 top planes
at scales A26, A27, A28 and A29 ; A29 is P^2 larger than A28.
Graphing A26 up to A29 had 3 interior rotating zones as a spiral staircase; d3
The reason the Lp's can not increase by exactly one, is that Lp(primesum) steps from less than one to over one,
based on the last prime integer added.
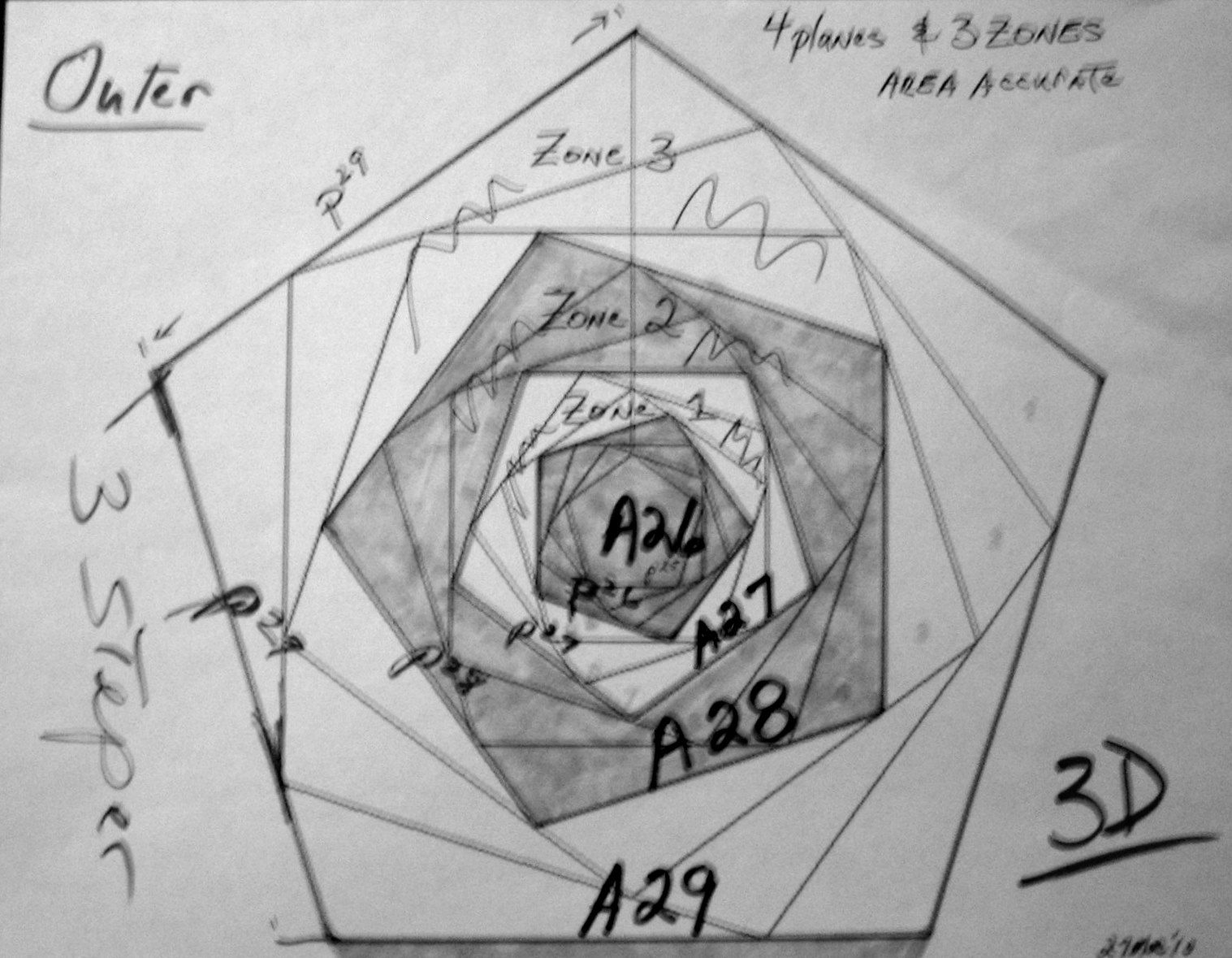
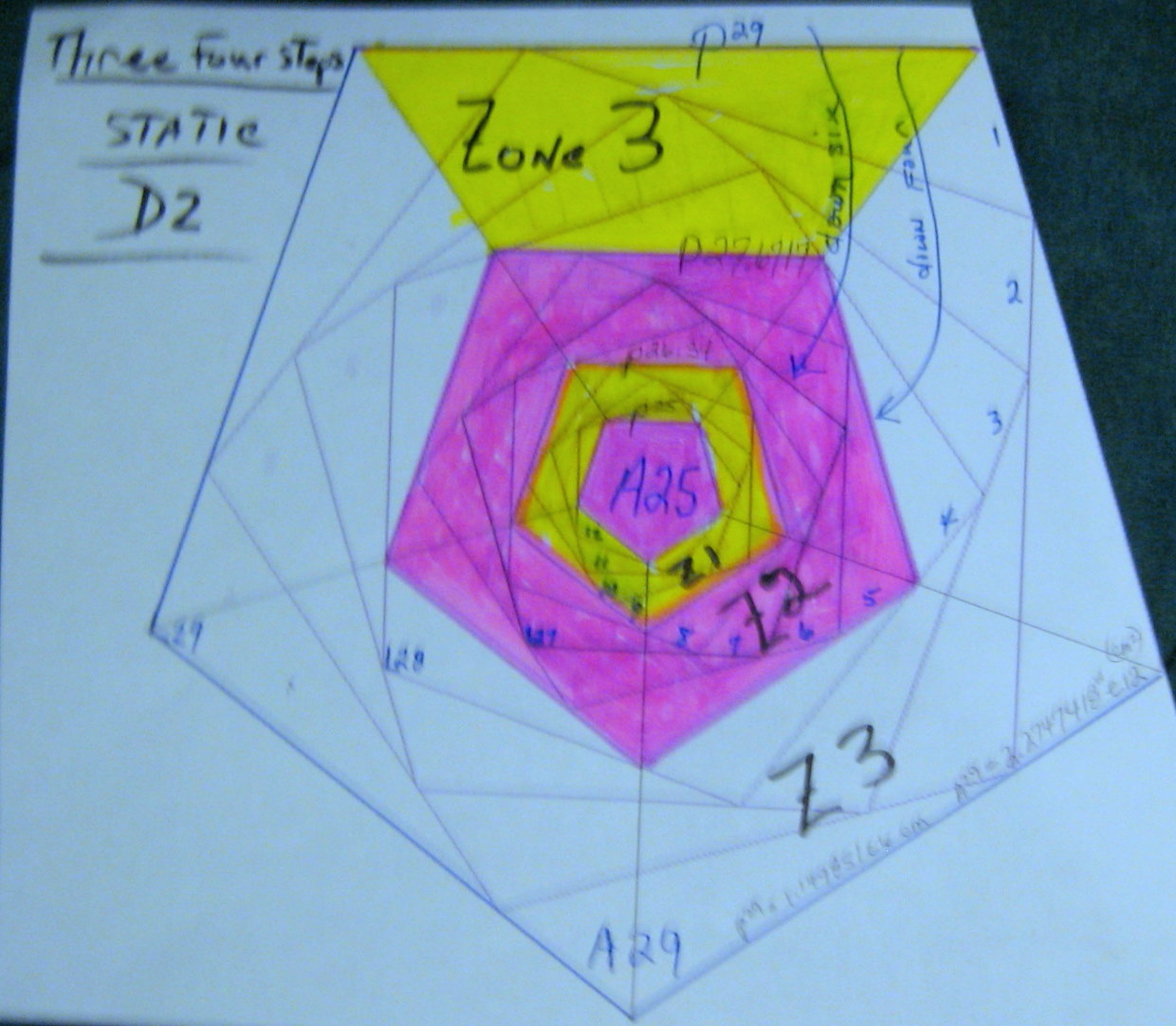
The 3D figure on the left illustrates the three zones between the four Top Planes.
While the 2D figure on the right shows a linear four step pattern between the last five Top Planes.
Conclusions
Both the three and four step Lp Patterns of the Prime Sums is clearly real and definitive!
These patterns will obviously go on indefinitely,
Therefore Prime Numbers and their distribution is self-evident, as witnessed by its Graphic Proof !!! [or QED]
It is amazing that PrimeNumberSums are simultaneously one, two and three dimensional in nature!
But only if you use the Golden ratio as your Log base does the pattern emerge.
Golden Ratio Logs
The Golden ratio was chosen because its has all three ratios simultaneously:
length increases by P^1=1.618... , area by P^2=2.618... and volume by P^3=4.23606... ;
also note that P^2 = P^1 + 1 and also that it is close to 'e' ,
and P^3 = 4 + P^-3 or 4 = P^3 - P^-3.
Lp is the log to base ( sqrt(5) 1) / 2 ) = 1.618.... Lp(X) = log( X ) / log(1.618....) .
Here are some common Lp examples/values:
Lp(123) = 10.000137.. ; and the inverse Px(10) = 122.991....
Lp(199) = 10.9999..., Lp(pi) = 2.37885~, Lp(e) = 2.078087~, Lp(2) = 1.44042~.
Px(7) = 29.03442~ , Lp(c) = 50.1313~ assuming P^0 = one centi-metre [cm]
Lucas numbers represent the integer steps of Px(n) series;
29, 47, 76, 123, 199 are the 7th, to 11th Lucas numbers.
Some spatial Perspectives
I have assigned an arbitrary scale and dimension to the powers of Px,
a one centimeter reference was selected for our human scale.
More likely, it was probably a fm scale or lower for nuclear geometry .
P^0 = 1 cm & P^12 is 322 cm, this makes P^29 equal to 1.149851e6 cm and
its area was A29 at 2.2747418~ e12 cm^2 .
I credit my Computer System Skills and Tools, along with my Geometrical insights, in making this discovery possible.
I am working on a "Geometry of the Prime Numbers" , based on these insights.
See my site for the latest material. WEB Site"
RD OMeara Oak Park IL 29March2010
---------------------------TABLE-------------------------------------
1ST 300 Million Prime Sums arranged by Lp, the log of the golden ratio!
16March2010 Author: RD_OMeara @ 60302 1.PrimeSums@Mister-Computer.Net
Step:25 PN/Step:0.000000 PN:97 Sum:1.060000E3 its Lp:14.476004 & Plane:A0.000000
Step:168 PN/Step:0.000000 PN:997 Sum:7.612700E4 its Lp:23.358026 & Plane:A0.000000
Step:1142 PN/Step:8.063923 PN:9209 Sum:4.901431E6 its Lp:32.013007 & Plane:A11.002360
------------ Note the four step sequences of "almost one" PN/Steps
Step:1430 PN/Step:8.344755 PN:11933 Sum:7.938735E6 its Lp:33.015117 & Plane:A11.336286
Step:1791 PN/Step:8.558906 PN:15329 Sum:1.285766E7 its Lp:34.017142 & Plane:A11.670360
Step:2244 PN/Step:8.841800 PN:19841 Sum:2.081248E7 its Lp:35.017975 & Plane:A12.003918
Step:2813 PN/Step:9.079630 PN:25541 Sum:3.369458E7 its Lp:36.019164 & Plane:A12.337553
Step:3527 PN/Step:9.331160 PN:32911 Sum:5.454920E7 its Lp:37.020316 & Plane:A12.671180
Step:4424 PN/Step:9.566682 PN:42323 Sum:8.827670E7 its Lp:38.020651 & Plane:A13.004574
Step:5551 PN/Step:9.826518 PN:54547 Sum:1.428682E8 its Lp:39.021139 & Plane:A13.337998
Step:6968 PN/Step:10.090270 PN:70309 Sum:2.312054E8 its Lp:40.021496 & Plane:A13.671369
Step:8749 PN/Step:10.329295 PN:90371 Sum:3.741730E8 its Lp:41.021912 & Plane:A14.004849
Step:10989 PN/Step:10.585950 PN:116329 Sum:6.054897E8 its Lp:42.022135 & Plane:A14.338229
Step:13806 PN/Step:10.828408 PN:149497 Sum:9.797281E8 its Lp:43.022188 & Plane:A14.671549
Step:17350 PN/Step:11.081210 PN:192259 Sum:1.585260E9 its Lp:44.022223 & Plane:A15.004855
Step:21811 PN/Step:11.335060 PN:247229 Sum:2.565107E9 its Lp:45.022306 & Plane:A15.338201
Step:27425 PN/Step:11.587566 PN:317789 Sum:4.150598E9 its Lp:46.022390 & Plane:A15.671566
Step:34496 PN/Step:11.842909 PN:408533 Sum:6.716063E9 its Lp:47.022469 & Plane:A16.004930
Step:43398 PN/Step:12.083253 PN:524389 Sum:1.086707E10 its Lp:48.022518 & Plane:A16.338276
Step:54612 PN/Step:12.341225 PN:673979 Sum:1.758381E10 its Lp:49.022579 & Plane:A16.671628
Step:68738 PN/Step:12.587783 PN:865259 Sum:2.845129E10 its Lp:50.022585 & Plane:A17.004955
Step:86537 PN/Step:12.839491 PN:1111091 Sum:4.603566E10 its Lp:51.022608 & Plane:A17.338294
Step:108970 PN/Step:13.092530 PN:1426693 Sum:7.448777E10 its Lp:52.022622 & Plane:A17.671627
Step:137244 PN/Step:13.341443 PN:1831033 Sum:1.205246E11 its Lp:53.022638 & Plane:A18.004967
Step:172893 PN/Step:13.593593 PN:2350237 Sum:1.950137E11 its Lp:54.022645 & Plane:A18.338301
Step:217836 PN/Step:13.841206 PN:3015113 Sum:3.155388E11 its Lp:55.022645 & Plane:A18.671632
Step:274517 PN/Step:14.091218 PN:3868279 Sum:5.105561E11 its Lp:56.022660 & Plane:A19.004971
---- Note the three Lp step sequences have a plus one Top Plane sequence
Step:346004 PN/Step:14.340248 PN:4961783 Sum:8.260999E11 its Lp:57.022667 & Plane:A19.338306
Step:436185 PN/Step:14.591600 PN:6364637 Sum:1.336660E12 its Lp:58.022671 & Plane:A19.671641
Step:549959 PN/Step:14.842039 PN:8162513 Sum:2.162767E12 its Lp:59.022677 & Plane:A20.004976
Step:693515 PN/Step:15.091917 PN:10466471 Sum:3.499432E12 its Lp:60.022677 & Plane:A20.338308
Step:874686 PN/Step:15.340530 PN:13418147 Sum:5.662201E12 its Lp:61.022677 & Plane:A20.671641
Step:1103334 PN/Step:15.590236 PN:17201237 Sum:9.161645E12 its Lp:62.022680 & Plane:A21.004975
Step:1391966 PN/Step:15.837275 PN:22044949 Sum:1.482387E13 its Lp:63.022682 & Plane:A21.338310
Step:1756332 PN/Step:16.087683 PN:28255313 Sum:2.398553E13 its Lp:64.022683 & Plane:A21.671643
Step:2216382 PN/Step:16.338229 PN:36211757 Sum:3.880941E13 its Lp:65.022683 & Plane:A22.004976
Step:2797290 PN/Step:16.585135 PN:46393433 Sum:6.279500E13 its Lp:66.022685 & Plane:A22.338310
Step:3530896 PN/Step:16.834681 PN:59441509 Sum:1.016044E14 its Lp:67.022685 & Plane:A22.671644
Step:4457435 PN/Step:17.082094 PN:76142323 Sum:1.643995E14 its Lp:68.022686 & Plane:A23.004977
Step:5627751 PN/Step:17.331403 PN:97536821 Sum:2.660041E14 its Lp:69.022686 & Plane:A23.338311
Step:7106165 PN/Step:17.579969 PN:124926157 Sum:4.304037E14 its Lp:70.022687 & Plane:A23.671644
Step:8973934 PN/Step:17.828289 PN:159989891 Sum:6.964080E14 its Lp:71.022687 & Plane:A24.004977
Step:11333855 PN/Step:18.076271 PN:204873829 Sum:1.126811E15 its Lp:72.022687 & Plane:A24.338311
Step:14315833 PN/Step:18.323737 PN:262319557 Sum:1.823220E15 its Lp:73.022687 & Plane:A24.671644
Step:18084223 PN/Step:18.572324 PN:335866043 Sum:2.950032E15 its Lp:74.022687 & Plane:A25.004977
Step:22846796 PN/Step:18.819933 PN:429975173 Sum:4.773252E15 its Lp:75.022687 & Plane:A25.338311
Step:28866367 PN/Step:19.067889 PN:550420693 Sum:7.723284E15 its Lp:76.022687 & Plane:A25.671644
Step:36475354 PN/Step:19.315144 PN:704526727 Sum:1.249653E16 its Lp:77.022687 & Plane:A26.004978
Step:46094125 PN/Step:19.563149 PN:901746253 Sum:2.021982E16 its Lp:78.022687 & Plane:A26.338311
Step:58254572 PN/Step:19.810411 PN:1154047031 Sum:3.271636E16 its Lp:79.022688 & Plane:A26.671644
Step:73629340 PN/Step:20.057806 PN:1476842981 Sum:5.293618E16 its Lp:80.022688 & Plane:A27.004978
Step:93069728 PN/Step:20.305086 PN:1889788871 Sum:8.565254E16 its Lp:81.022688 & Plane:A27.338311
Step:117652380 PN/Step:20.552306 PN:2418027719 Sum:1.385887E17 its Lp:82.022688 & Plane:A27.671644
Step:148739879 PN/Step:20.799302 PN:3093685613 Sum:2.242412E17 its Lp:83.022688 & Plane:A28.004978
Step:188056076 PN/Step:21.046210 PN:3957867593 Sum:3.628300E17 its Lp:84.022688 & Plane:A28.338311
Step:237782434 PN/Step:21.293294 PN:5063171261 Sum:5.870712E17 its Lp:85.022688 & Plane:A28.671644
Step:300679579 PN/Step:21.540163 PN:6476687027 Sum:9.499013E17 its Lp:86.022688 & Plane:A29.004978
-end- Step:301000000 Prime:6483922183 Sum:9.519777E17 Lp:86.027225 idx:61 Base=27.000000 bias=0.000000
Appendix: Volume and Scale
Let a cubic centimeter [or cc = cm^3] be the standard volume unit. On our human scale, this small sugar cube sized item seems small and ordinary.
What does Mercury's orbital volume of 8e23 cubic KM and the nuclear volume have in common
with this standard cm^3 ?
Both are equally distant from a standard cubic centimeter;.
Imagine a cc as the mid zone between Nuclear and Planetary Orbit scales.
This means the volume of Mercury's orbit is as distant as the volume of a nucleus when using a cc reference volume.
Compare it at whatever precision imaginable.
Pause to consider how planetary orbital volumes makes any human scale volume seem insignificant;
whether its a cc or a cubic mile.
Can any basis of linearity be possible or even imaginable at these vast ranges?
Surely VOLUME at the Nuclear scale would be a thing onto itself.
Normal spatial concepts of our macro scale would seem not apply over such a scale distance.
Users of Nano technology are familiar with non-linear scale effects that redefine our common macro sense of volume; eg static electricty.
LINKS 
author: RD O'Meara Oak Park, IL.
This WEB page address: "http://mister-computer.net/primesums/primesums.htm"
Email of Author: 'RDo.meara@mister-computer.net'
JID's SLOPE: The Universal Slope of Volume, Mathematically and Physically.
AKA, the Rydberg constant of 1.0973~!
5SPACE: "Particle Mass mapped by (N/2)^5, N=1 to 22"
My Real interests are in computer science, I have spent my career as a cybernetic engineer/designer who
is concerned about the future of our digital data. Our entire cyber infrastructure lacks "Data Sanity";
especially in the areas of forgery and security, for data and time stamps.
In that vein, I have designed a NEW multi-Computer SECURE Operating System,
aka Posopip - a 3CPU system
HEDRONS : A slide show of 'The new 1-2-3 Digital Method of Counting in Three Dimensions!
5SPACE in MySpace
28March2010
